主成分分析 不但是多元统计分析的重要部分，而且在日常的数据分析工作中也发挥着重要作用。以下详细介绍主成分分析的原理和R语言实践。

PCA有什么用？

主成分分析 （principal component analysis）简称 PCA，主要通过变量的降维，将复杂问题简单化，方便理解现状及进一步分析。降维的思想很常见，以均值为例，由于我们无法理解较多数字的含义，用一个均值来表达较多数字的信息，这就是很朴素的降维思想。

举个例子，以下是几个学生各科的成绩。我们很容易得出 学生成绩的好坏主要由数学和物理决定 的结论。其实这个结论已经蕴含了主成分分析的思想，将4个变量简化为2个，复杂的问题变的简单

学生	语文	数学	英语	物理
A	90	100	110	80
B	90	90	110	90
C	90	140	110	100
D	90	150	110	85
E	90	70	110	65
F	90	65	110	75
G	90	105	110	85
H	90	125	110	95

但是各科成绩变为以下数据，结论还能轻易得出吗？

学生	语文	数学	英语	物理
A	55	100	110	80
B	65	90	100	90
C	95	140	90	100
D	120	150	75	85
E	140	70	130	65
F	80	65	99	75
G	99	105	105	85
H	95	125	110	95

现在就能体现主成分分析的价值了，主成分与指标的关系如下：

主成分是原始变量的线性组合
主成分的个数要小于原始变量的个数
主成分保留了原始变量的大部分信息
各个主成分互不相关

PCA的原理

PCA的几何原理

要描述如下的原始数据，需要x和y两个指标，如果将坐标轴做个旋转，保留长轴信息舍弃短轴信息，那么就可以用一个指标描述原始数据，在尽量保留信息的情况下，简化了指标。

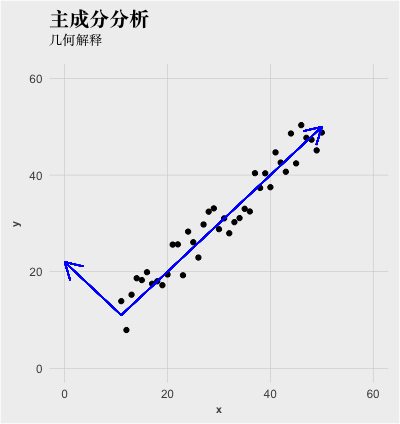
主成分分析的本质就是进行坐标系的旋转，各个主成分就是新坐标系和原坐标系的转换关系。

PCA的统计学原理

统计学求解主成分，一般用 最大方差法 ，很容易理解，我们原始数据的投影能尽量包含原始数据的信息，这就要求投影分散的最开，反映到公式上就是方差最大。

有 $p$ 维随机向量 $\textbf{X} = {\left ( X_{1},X_{2},\cdot \cdot \cdot ,X_{p} \right )}’$ ，随机向量 $\textbf{X}$ 的协方差矩阵为 $\Sigma$

对 $\textbf{X}$ 进行线性变换，形成新的综合变量，用 $\textbf{Y}$ 来表示，即

$\left\{ \begin{array}{c} Y_{1} = u_{11}X_{1} + u_{21}X_{2} + \cdot \cdot \cdot +u_{p1}X_{p} \\ Y_{2} = u_{12}X_{1} + u_{22}X_{2} + \cdot \cdot \cdot +u_{p2}X_{p} \\ \cdot \cdot \cdot \cdot \cdot \cdot \\ Y_{p} = u_{1p}X_{1} + u_{2p}X_{2} + \cdot \cdot \cdot +u_{pp}X_{p} \end{array} \right.$

目标是 $Y_{i} = \textbf u_{i}’ \textbf X$ 的方差尽可能大，且各 $Y_{i}$ 之间互不相关

由于 $var(Y_{i}) = var(\textbf u_{i}’ \textbf X) = \textbf u_{i}’ \Sigma \textbf u_{i}$ 可以任意大，问题变的没有意义。所以增加约束条件 $\textbf u_{i}’ \textbf u_{i} = 1 $

问题变为：

$\begin{cases} max & \textbf u_{i}' \Sigma \textbf u_{i} \\ s.t. & \textbf u_{i}' \textbf u_{i} = 1 \end{cases}$

引入拉格朗日乘子，将求最大方差问题变为求 $f$ 的平稳点

$f(u,\lambda ) = {u}'\Sigma u + \lambda(1-{u}'u)$

对 $f$ 求偏导，得

$\begin{cases} \frac{\partial f}{\partial u} = 2\Sigma u - 2\lambda u = 0 \\ \frac{\partial f}{\partial \lambda} = 1 - {u}'u = 0 \end{cases}$

得

$\begin{cases} \Sigma u - \lambda u = 0 \\ 1 - {u}'u = 0 \end{cases}$

很神奇的是，问题变为求 $\Sigma $ 的特征值

且 ${u}’ \Sigma u = {u}’ \lambda u = \lambda {u}’ u = \lambda$

求最大方差变成了求最大特征值

note: 以上是从协方差阵出发，还有从相关阵出发的情况，可以证明原始数据的相关阵就是对原始数据标准化后的协方差阵

特征值求解见附录

PCA的R语言实践

USJudgeRatings数据集记录了律师对美国高等法院法官的评分，包括12个维度，数据如下：

> head(USJudgeRatings)
               CONT INTG DMNR DILG CFMG DECI PREP FAMI ORAL
AARONSON,L.H.   5.7  7.9  7.7  7.3  7.1  7.4  7.1  7.1  7.1
ALEXANDER,J.M.  6.8  8.9  8.8  8.5  7.8  8.1  8.0  8.0  7.8
ARMENTANO,A.J.  7.2  8.1  7.8  7.8  7.5  7.6  7.5  7.5  7.3
BERDON,R.I.     6.8  8.8  8.5  8.8  8.3  8.5  8.7  8.7  8.4
BRACKEN,J.J.    7.3  6.4  4.3  6.5  6.0  6.2  5.7  5.7  5.1
BURNS,E.B.      6.2  8.8  8.7  8.5  7.9  8.0  8.1  8.0  8.0
               WRIT PHYS RTEN
AARONSON,L.H.   7.0  8.3  7.8
ALEXANDER,J.M.  7.9  8.5  8.7
ARMENTANO,A.J.  7.4  7.9  7.8
BERDON,R.I.     8.5  8.8  8.7
BRACKEN,J.J.    5.3  5.5  4.8
BURNS,E.B.      8.0  8.6  8.6

目标是把12个维度综合成几个主成分，在尽量保留信息的前提下实现降维

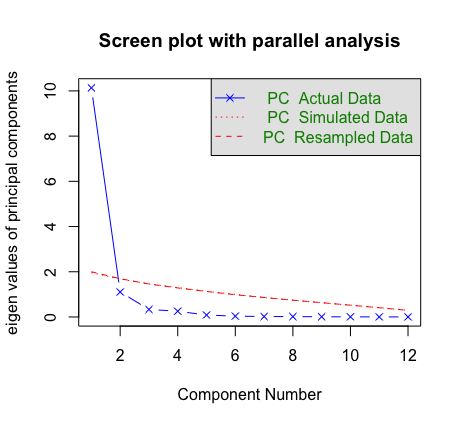
1 2	# 判断主成分的个数 fa.parallel(USJudgeRatings,fa="pc",n.iter=100,show.legend=T,main="Screen plot with parallel analysis")

从蓝线看出，在2->3时，特征值变化放缓；从红线看出，红线以上的特征值对应的主成分是1。所以此例选择1个或2个主成分都是合理的，这里我们选2个主成分

从以下结果看出：

R基于相关阵计算主成分
2个主成分解释了94%的方差
h2列为主成分对单个变量的解释程度，本例的解释程度都很强
PC1和PC2的系数是主成分载荷（loadings），指主成分和变量的相关系数
SS loadings为特征值
Cumulative Var为主成分对数据的解释程度

> pc = principal(USJudgeRatings,
+                nfactors=2,
+                rotate = "none")
> pc
Principal Components Analysis
Call: principal(r = USJudgeRatings, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrix
       PC1   PC2   h2     u2 com
CONT -0.01  0.98 0.96 0.0390 1.0
INTG  0.92 -0.19 0.88 0.1197 1.1
DMNR  0.91 -0.21 0.88 0.1229 1.1
DILG  0.97  0.04 0.94 0.0599 1.0
CFMG  0.96  0.18 0.96 0.0410 1.1
DECI  0.96  0.13 0.94 0.0584 1.0
PREP  0.98  0.03 0.97 0.0287 1.0
FAMI  0.98  0.00 0.95 0.0469 1.0
ORAL  1.00  0.00 0.99 0.0091 1.0
WRIT  0.99 -0.03 0.98 0.0184 1.0
PHYS  0.89  0.09 0.81 0.1927 1.0
RTEN  0.99 -0.04 0.97 0.0258 1.0
                        PC1  PC2
SS loadings           10.13 1.10
Proportion Var         0.84 0.09
Cumulative Var         0.84 0.94
Proportion Explained   0.90 0.10
Cumulative Proportion  0.90 1.00
Mean item complexity =  1
Test of the hypothesis that 2 components are sufficient.
The root mean square of the residuals (RMSR) is  0.03
 with the empirical chi square  4.46  with prob <  1
Fit based upon off diagonal values = 1

以下是主成分得分的系数

> pc$weights
               PC1          PC2
CONT -0.0009660187  0.887804400
INTG  0.0906447029 -0.173243022
DMNR  0.0901211706 -0.188017467
DILG  0.0956091216  0.034550076
CFMG  0.0950495297  0.160255129
DECI  0.0948356759  0.121697038
PREP  0.0971962573  0.030672573
FAMI  0.0963396287 -0.001251621
ORAL  0.0982335093 -0.003450490
WRIT  0.0977160877 -0.029862233
PHYS  0.0881858990  0.084734541
RTEN  0.0973168144 -0.037478023

PC1 = -0.0009660187CONT + 0.0906447029INTG +…+ 0.0973168144RTEN
PC2 = ……

附录

特征值求解示例

原始矩阵如下，用初等行列变换，求解特征值

$\begin{bmatrix} 2 & -1 & 1 \\ 0 & 3 & -1 \\ 2 & 1 & 3 \\ \end{bmatrix}$

第一步，$\lambda $ 减去对角线元素，其余元素变负

$\begin{bmatrix} \lambda - 2 & 1 & -1 \\ 0 & \lambda - 3 & 1 \\ -2 & -1 & \lambda - 3 \\ \end{bmatrix}$

第二步，第1列和第3列互换

$\begin{bmatrix} -1 & 1 & \lambda - 2 \\ 1 & \lambda - 3 & 0 \\ \lambda - 3 & -1 & -2 \\ \end{bmatrix}$

第三步，第1列乘 $\lambda - 2$ 加到第3列

$\begin{bmatrix} -1 & 1 & 0 \\ 1 & \lambda - 3 & \lambda - 2 \\ \lambda - 3 & -1 & \lambda^{2} - 5\lambda + 4 \\ \end{bmatrix}$

第四步，第1列加到第2列

$\begin{bmatrix} -1 & 0 & 0 \\ 1 & \lambda - 2 & \lambda - 2 \\ \lambda - 3 & \lambda - 4 & \lambda^{2} - 5\lambda + 4 \\ \end{bmatrix}$

第五步，第2列乘-1加到第3列

$\begin{bmatrix} -1 & 0 & 0 \\ 1 & \lambda - 2 & 0 \\ \lambda - 3 & \lambda - 4 & (\lambda - 4)(\lambda - 2) \\ \end{bmatrix}$

第六步，对角线元素乘积等于0

$(\lambda - 4)(\lambda - 2)(\lambda - 2) = 0$

特征值 $\lambda_{1} = \lambda_{2} = 2 ,\lambda_{3} = 4$