R语言与svm分类

发表于 | 分类于

支持向量机(support vector machine)缩写为”svm”，是机器学习方法的重要组成。本文介绍用R语言解决svm分类的流程

svm简介

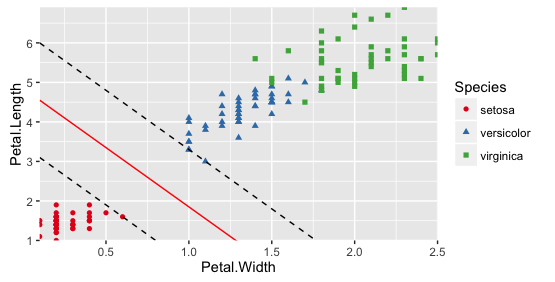
假如想要将iris数据集的setosa和versicolor分开，有无数种方法（有无数条直线或者曲线）。但似乎 红色这条线 的鲁棒性最强，对点波动的容忍度更高，而且直观上看，红色这条线 也在两堆点的正中间。

函数间隔

假设超平面 $f(x) = w^{T}x + b$ ，当f(x)>0时，y为正类(+1)，f(x)<0时，y为反类(-1)。而且分类正确的条件是，f(x)和y同号，即 $f(x)y$ 为正。则定义 函数间隔 为 $\widehat{\gamma }=y(w^{T}x + b) = yf(x)$ 。由于w和b同时变动时，超平面不变 $(w^{T}x + b = 0)$ ，但是 函数间隔 会变化，所以函数衡量只能衡量分类是否正确，无法找出最完美的分割线。下面引出 几何间隔 ，能很好的解决这个问题

几何间隔

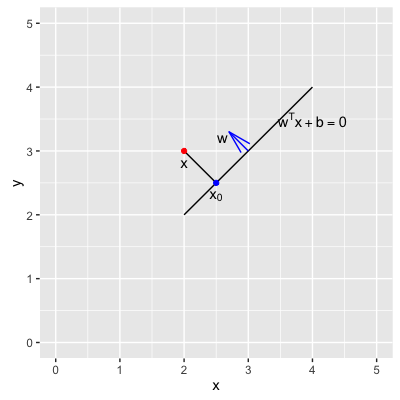
如上图所示，r是x0到x的距离，$(w^{T}x + b = 0)$ 是超平面，w是法向量。则

$\left | w \right |$ 是单位长度的法向量，也称为 模

上式两边同乘以 $w^{T}$，可得 $w^{T}x = w^{T}x_{0} + r\frac{w^{2}}{\left | w \right |}$ ，由于x0在超平面上，所以 $w^{T}x_{0}+b=0$ ，则 $\gamma =\frac{w^{T}x+b}{\left | w \right |}=\frac{f(x)}{\left | w \right |}$ ，但 $\gamma$ 有可能为负，将绝对值 $\gamma$ 写为：

可以清楚的看到 几何间隔 不会随着w和b的变化而改变，最大间隔分类超平面中的 间隔 指的是几何间隔。

最大间隔分类器

最大间隔分类器的目标函数变成：$max \widehat{\gamma }$ ，同时满足 $y_{i}(w^{T}x_{i}+b)= \widehat{\gamma _{i}} \geqslant \widehat{\gamma }$

如果令函数间隔 $\widehat{\gamma } = 1$ ，则目标函数变为 $max\frac{1}{\left | w \right |}$ 且 $y_{i}(w^{T}x_{i}+b) \geqslant 1$ ，满足的 $y_{i}(w^{T}x_{i}+b) = 1$ 的点称为 支持向量

R包实现

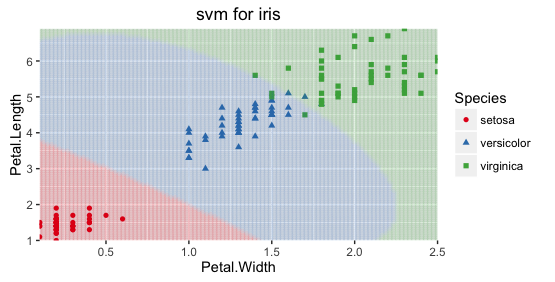
用SVM将iris数据集的setosa、versicolor、virginica分类，下图的分类边界即是 支持向量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# svm实现iris数据集分类
iris_subset = iris[,3:5] # 筛选Petal.Length,Petal.Width,Species
model = svm(Species~.,iris_subset) # svm model
iris_subset$svmpre = predict(model) # svm预测值，等同于fit
gridRange = apply(iris_subset[c('Petal.Width','Petal.Length')],2,range) #两个变量的最大和最小值
x1 = seq(gridRange[1,1],gridRange[2,1],by=(gridRange[2,1]-gridRange[1,1])/100)
x2 = seq(gridRange[1,2],gridRange[2,2],by=(gridRange[2,2]-gridRange[1,2])/100)
grid = expand.grid(Petal.Width = x1,Petal.Length = x2)
grid$class = predict(model,grid)
ggplot(NULL) +
  geom_point(data = iris_subset,
             aes(Petal.Width,Petal.Length,
                 color = Species,
                 shape = Species)) +
  geom_point(data = grid,
             aes(Petal.Width,Petal.Length,
                 color = as.factor(class)),
             size = 1.5,
             alpha = 0.05,
             show.legend = FALSE) +
  scale_color_brewer(palette = "Set1") +
  scale_x_continuous(expand = c(0,0)) +
  scale_y_continuous(expand = c(0,0)) +
  ggtitle("svm for iris")
喂他一颗糖